1. ຄວາມເຂົ້າໃຈຂະບວນການບິດ: ຂໍ້ເທັດຈິງງ່າຍດາຍ
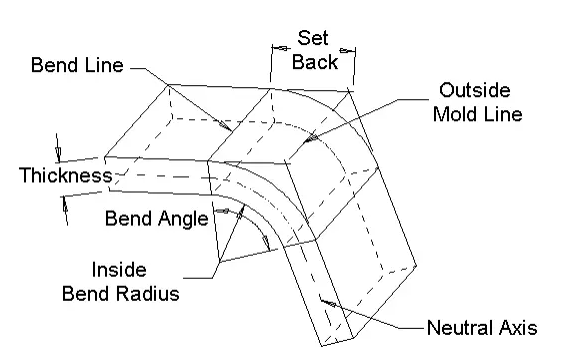
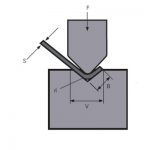
Bend Allowance = Angle * (T/ 180)*(Radius + K-factor * Thickness)Bend Compensation = Bend Allowance-(2 * Set Back)
Inside Set Back = tan (Angle / 2) *Radius Outsideset Back = tan (Angle / 2)*(Radius + Thickness)

1) ລັດສະໝີທີ່ໄດ້ຮັບໃນສ່ວນທີ່ງໍສົ່ງຜົນກະທົບຕໍ່ຄວາມຍາວທີ່ພວກເຮົາຕ້ອງຕັດສ່ວນນັ້ນ (ກ່ອນທີ່ຈະງໍ).
2) radius ທີ່ໄດ້ຮັບໃນ bending ແມ່ນຂຶ້ນກັບ 99% ກ່ຽວກັບການເປີດ V ພວກເຮົາເລືອກທີ່ຈະເຮັດວຽກຮ່ວມກັບ.
ກ່ອນທີ່ຈະອອກແບບພາກສ່ວນແລະແນ່ນອນກ່ອນທີ່ຈະເລີ່ມຕັດຊ່ອງຫວ່າງ, ພວກເຮົາຕ້ອງຮູ້ຢ່າງແທ້ຈິງວ່າ V ເປີດທີ່ພວກເຮົາຈະໃຊ້ເພື່ອງໍພາກສ່ວນເທິງເບກກົດ.
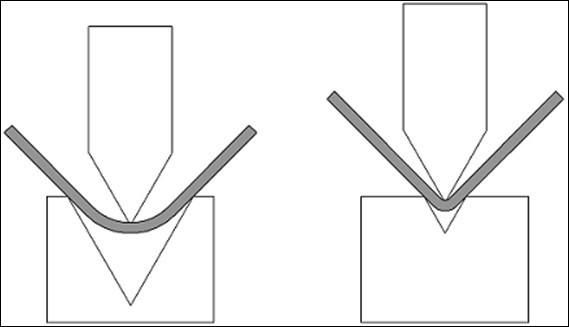
2. ລັດສະໝີມີຜົນກະທົບແນວໃດກັບຊ່ອງຫວ່າງ
ລັດສະໝີທີ່ໃຫຍ່ກວ່າຈະ "ຍູ້" ຂາຂອງສ່ວນຂອງພວກເຮົາໄປສູ່ດ້ານນອກ, ເຮັດໃຫ້ຄວາມຮູ້ສຶກທີ່ຫວ່າງເປົ່າຖືກຕັດ "ຍາວເກີນໄປ".
ລັດສະໝີທີ່ນ້ອຍກວ່າຈະຕ້ອງການຊ່ອງຫວ່າງທີ່ຕ້ອງຕັດ “ຍາວໜ້ອຍໜຶ່ງ” ກ່ວາຖ້າລັດສະໝີໃຫຍ່ກວ່າ.
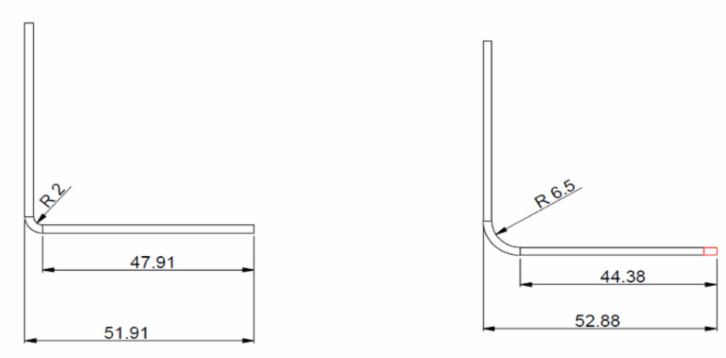
3. ເງິນອຸດໜູນ
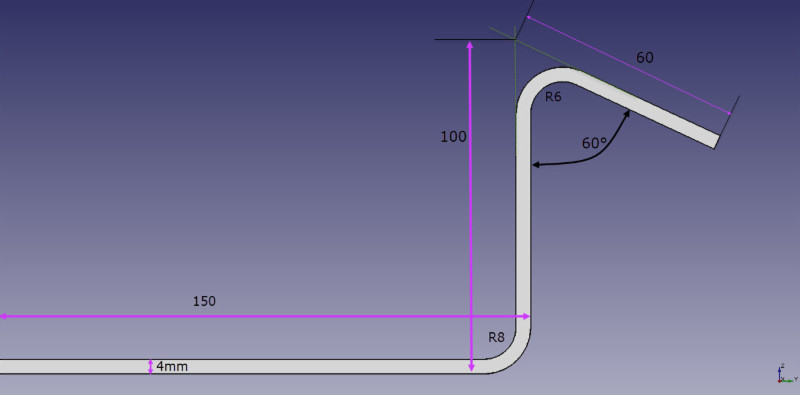
ຊ່ອງຫວ່າງທີ່ເປີດເຜີຍຂອງຕົວເລກຂ້າງເທິງນີ້ຈະຖືກຄິດໄລ່ດັ່ງຕໍ່ໄປນີ້:
B = 150 + 100 + 60 + BA1 + BA2
ວິທີການຄິດໄລ່ BA1 ແລະ BA2:
ການຄິດໄລ່ເງິນອຸດໜູນງໍ
ສ່ວນທີ່ພວກເຮົາຈໍາເປັນຕ້ອງໄດ້ຫຼຸດລົງຈາກຂາທັງສອງຄັ້ງທີ່ທັບຊ້ອນກັນໂດຍການກາຍເປັນຮາບພຽງ, ແມ່ນສິ່ງທີ່ພວກເຮົາຮູ້ທົ່ວໄປວ່າ "ເງິນອຸດໜູນ" (ຫຼື BA ໃນສົມຜົນ).
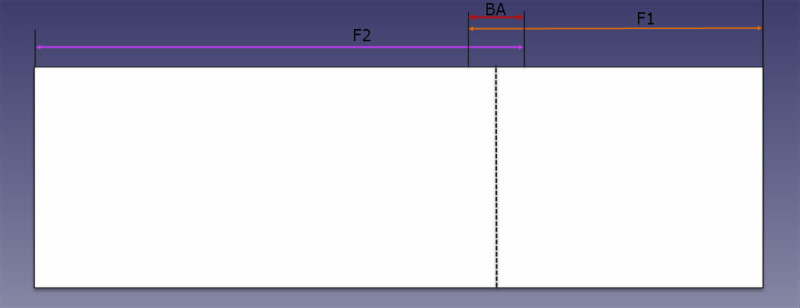
ສູດການອະນຸຍາດບິດ
ສູດ BA ສໍາລັບການງໍເຖິງ 90°
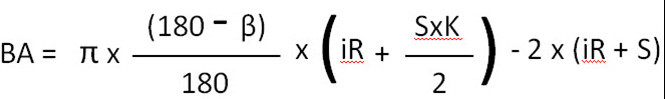
ສູດ BA ສໍາລັບງໍຈາກ 91° ຫາ 165°
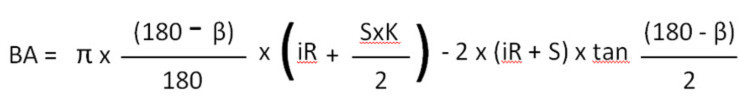
iR=ລັດສະໝີພາຍໃນ
S=ຄວາມໜາ
Β = ມຸມ
Π = 3,14159265….
K = ປັດໄຈ K
ປັດໄຈ K
ເມື່ອງໍໃສ່ເບກກົດ, ສ່ວນດ້ານໃນຂອງແຜ່ນໂລຫະຈະຖືກບີບອັດໃນຂະນະທີ່ດ້ານນອກຖືກຂະຫຍາຍອອກ.
ນີ້ຫມາຍຄວາມວ່າມີສ່ວນຫນຶ່ງຂອງແຜ່ນທີ່ເສັ້ນໄຍບໍ່ໄດ້ຖືກບີບອັດຫຼືຂະຫຍາຍອອກ. ພວກເຮົາເອີ້ນພາກສ່ວນນີ້ວ່າ "ແກນກາງ."
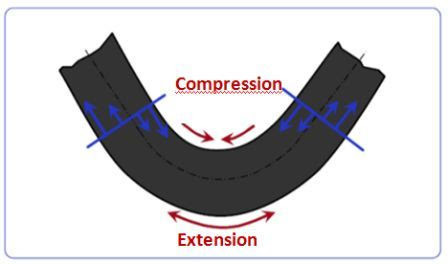
ໄລຍະຫ່າງຈາກພາຍໃນຂອງໂຄ້ງໄປຫາແກນກາງແມ່ນສິ່ງທີ່ພວກເຮົາເອີ້ນວ່າປັດໄຈ K.
ມູນຄ່ານີ້ມາພ້ອມກັບວັດສະດຸທີ່ພວກເຮົາຊື້ແລະມັນບໍ່ສາມາດປ່ຽນແປງໄດ້.
ຄ່ານີ້ສະແດງອອກເປັນເສດສ່ວນ. ປັດໄຈ K ທີ່ນ້ອຍກວ່າ, ແກນກາງຈະຢູ່ໃກ້ກັບລັດສະໝີພາຍໃນຂອງແຜ່ນ.
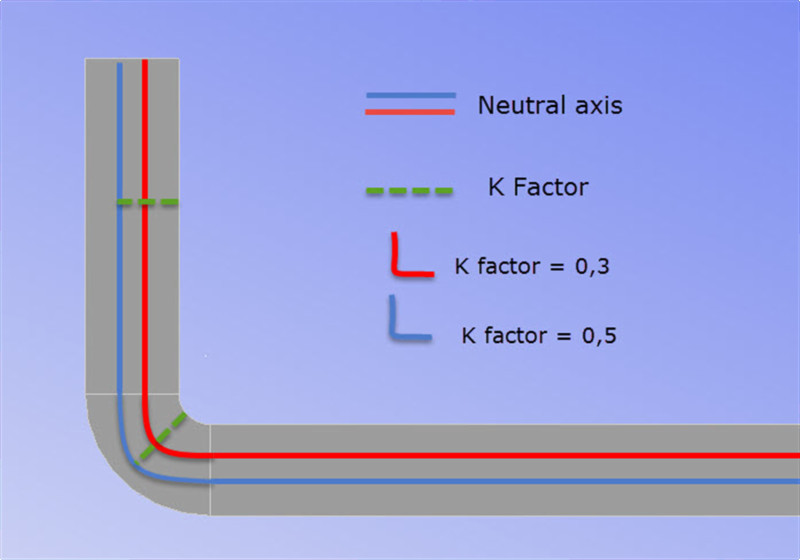
K factor = ການປັບລະອຽດ
ປັດໄຈ K ຜົນກະທົບຕໍ່ການເປີດເຜີຍຂອງພວກເຮົາ. ບໍ່ຫຼາຍເທົ່າກັບລັດສະໝີຂອງພາກສ່ວນ, ແຕ່ພວກເຮົາສາມາດຄິດວ່າມັນເປັນການຄິດໄລ່ການປັບລະອຽດສໍາລັບຊ່ອງຫວ່າງ.
ປັດໄຈ K ຂະຫນາດນ້ອຍກວ່າ, ວັດສະດຸຫຼາຍແມ່ນຂະຫຍາຍອອກແລະດັ່ງນັ້ນ "ຖືກຍູ້ອອກ"…. ຊຶ່ງຫມາຍຄວາມວ່າຂາຂອງພວກເຮົາຈະກາຍເປັນ "ໃຫຍ່ຂຶ້ນ".
ການຄາດຄະເນປັດໄຈ K
ສ່ວນໃຫຍ່ຂອງເວລາທີ່ພວກເຮົາສາມາດຄາດຄະເນແລະປັບຕົວປັດໄຈ K ໃນເວລາທີ່ປັບການຄິດໄລ່ເປົ່າຂອງພວກເຮົາ.
ທັງຫມົດທີ່ພວກເຮົາຕ້ອງການຈະເຮັດແມ່ນບາງການທົດສອບ (ກ່ຽວກັບການເປີດ V ໄດ້ຄັດເລືອກ) ແລະວັດແທກ radius ຂອງສ່ວນ.
ໃນກໍລະນີທີ່ທ່ານຕ້ອງການກໍານົດປັດໄຈ K ທີ່ຊັດເຈນກວ່າ, ຂ້າງລຸ່ມນີ້ແມ່ນການຄິດໄລ່ສໍາລັບການກໍານົດປັດໄຈ K ທີ່ແນ່ນອນສໍາລັບການງໍຂອງທ່ານ.

ປັດໄຈ K: ສູດ
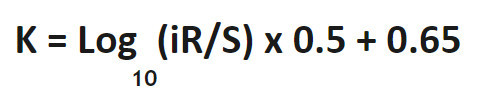
ການແກ້ໄຂຕົວຢ່າງ:
B = 150 + 100 + 60 +BA1 + BA2
ການຄາດຄະເນປັດໄຈ K
B1: R/S=2 => K=0,8
B2: R/S=1,5 => K=0,8
ທັງສອງງໍແມ່ນ 90° ຫຼືນ້ອຍກວ່າ:
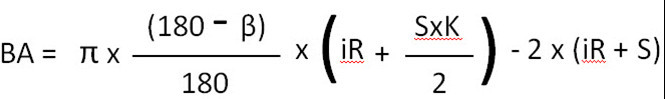
ຫມາຍຄວາມວ່າ:
B1 = 3.14 x 0.66 x (6 + ((4 × 0.8)/2) – 2 x 10
B1 = −4.25
B2 = 3.14 x 0.5 x (8 + ((4 × 0.8)/2) – 2 x 12
B2 = −8.93
ດັ່ງນັ້ນ:
B = 150 + 100 + 60 + (−4.25) + (−8.93)
B=296.8ມມ